Метод решения судоку Wings

Внимание!!!

Эта страница находится в Разработке. Вопросы и предложения принимаются через ресурсы в разделе Общение.

Описание алгоритма. Примеры Wings.

Введение

Для лучшего понимания метода представьте себе птицу. А лучше насекомое, у которого может быть более двух крыльев (в том числе и нечетное количество). При этом каждое крыло должно быть уникальным, не похожим на остальные. И обязательно одно неправильное крыло.

Рис. 1. Стрекоза (Dragonfly)

Существующая классификация

Считается, что к семейству методов Wings относится:

1. X-Wings
2. XY-Wings (он же Y-Wings)
3. XYZ-Wings
4. WXYZ-Wings (Type 1, Type 2)
5. W-Wings

---

Но давайте разбираться дальше.

Введем несколько определений.

Wings (Крылья)

Историю появления этого термина в судоку не нашел. Мое предположение, что произошло от сопоставления метода с птицей/насекомым. У которой есть туловище и крылья. Применительно к судоку получается, что крыльев у птицы может быть больше двух и даже нечетноей количество.

Крыло может проходить через несколько клеток в одном секторе, но с одним кандидатом. Крыло должно должно быть уникальным. Т.е. если два крыла с одним кандидатом в разных секторах, то это уже не крыло, вернее тогда этот метод нельзя применить.

Другими словами крылья (wings) - это не только линки links (сильные или слабые линки) они могут проходить через несколько клеток в секторе, но начинаться они должны из одной ячейки (туловища).

Крылья могут быть:

• X-Wing - Крыло по кандидату X
• Y-Wing - Крыло по кандидату Y
• Z-Wing - Крыло по кандидату Z

Правильное крыло

Правильное крыло - взаимосвязанные узлы по одному кандидату, начинающиеся в Базе. Узлы должны находиться в одном секторе любого типа. При этом в крыле может быть только один правильный любой узел, исключающий все остальные.

Неправильное крыло | (возможно "Сломанное крыло")

Неправильное крыло - взаимосвязанные узлы по одному кандадату, которые занимают как минимум два сектора каждого типа.

Проверяемый кандидат |

Проверяемый кандидат - кандидат в неправильном крыле. Для него нужно будет искать общих соседей для исключения.

База | Основа | Туловище

База - место откуда будут выходить крылья.

Для некоторых методов Wings база отсутствует.

База может быть:

1. Свободной ячейкой
2. Две свободные ячейки, находящиеся на пересечении одной линии и одного бокса
3. Три свободные ячейки, находящиеся на пересечении одной линии и одного бокса
4. Сильный/Слабый Линк по кандидату

Примеров, где базой является несколько ячееек не приведено, т.к. поиск таких решений является очень ресурсоёмким для машин (тем более для человека). Возможно, позднее займусь этим вопросом.

Суть методов Wings

Есть одна/несколько свободных ячейка, назовем это База (туловище птицы) из которой будут начинаться крылья (wings).

Из этой Базы "растут" крылья (wings) по кандидатам.

Важно отметить, что крылья должны быть уникальными, т.е. по одному крылу с каждым кандидатом, кроме одного (преверяемого кандидата), по которому будут искаться и при нахождении удаляться общие соседи.

Т.о. крылья могут расти по соседним свободным клеткам относительно Базы общей по строке, столбцу и боксу.

Давайте называть узлы-кандидаты в Базе - начало крыла, соответственно другой конец - окончание крыла.

Задействованные клетки - базовые ячейки и ячейки с окончанием крыльев.

Конечные-Ячейки - ячейки с окончанием крыльев.

Задействованные кандидаты - кандидаты в задействованных клетках.

Правила для Wings:

• Крылья строятся из Базы до Конечных ячеек.
• Для кандидата из опорной точки должно быть только одно крыло.

Главное правило методов Wings - Количество задействованных кандидатов, должно совпадать с количеством задействованных клеток.

Крылья из опорной точки для каждого кандидато

Если взять N - размер крыльев для метода.

N (Количество крыльев)	Название
1	X-Wings
2	XY-Wings
3	XYZ-Wings
4	XYZW-Wings
5	XYZWV-Wings

Для метода N-Wings из одной клетки, имеющей N и меньше кандидатов, должно выходить крыльев к другим клеткам. Количество простых крыльев (с одним кандидатов) должно совпадать с количеством задейстованных клеток в крыльях.

Символы в названии XYZW

Символы XYZW в названиях методов обозначают цифру для участвующих кандидатов.

Предложение по классификации методов

Возможно более правильно классифицировать методы Wings по форме основы (базы, туловища) и количеству крыльев.

Форма туловища:

1. Одная ячейка
2. Две ячейки
3. Три ячейки
4. Сильный линк

Количество крыльев

1. Два крыла
2. Три крыла
3. Четыре крыла
4. Пять крыльев
5. Шесть крыльев
6. Семь крыльев
7. Восемь крыльев

Пока основным критерием для классификации мне кажется количество крыльев. Поэтому логично использование Wing-N, где N - количество крыльев.

Но рассмотрим общепринятую классификацию по порядку.

X-Wings

Метод опирается на два крыла (сильных линка) одного кандидата, расположенных по двум противоположным сторонам прямоугольника.

Рис. 1.1. Biplane

Мнения по классификации этого метода расходятся. Кто-то считает, что это Fishes (Рыбы), кто-то что AIC (Nice loop), а кто-то считает, что названо потому-что похоже на космический корабль из фильма "Звездные войны" или Биплан.

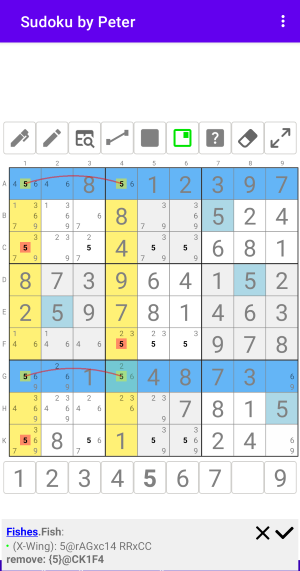Рис. 1.2. X-Wings

На мой взгляд это чистейшая Рыба размера 2.

Fishes:Fish (X-Wing): 5@rAGxc14 RRxCC remove: {5}@CK1F4

XY-Wings | Y-Wings

Признаки метода XY-Wings:

1. Используюся три свободных ячейки.
2. Одна базовая, из которой начинаются правильные крылья. В этом методе крылья могут быть только линками (сильными или слабыми)
3. Базовая ячейка содержит только кандидатов из правильных крыльев.
4. Две свободные ячейки с окончаниями крыльев.
5. Есть одно неправильное крыло.
6. Все узлы неправильного крыла имеют как минимум одного общего соседа. Эти узлы можно удалять.

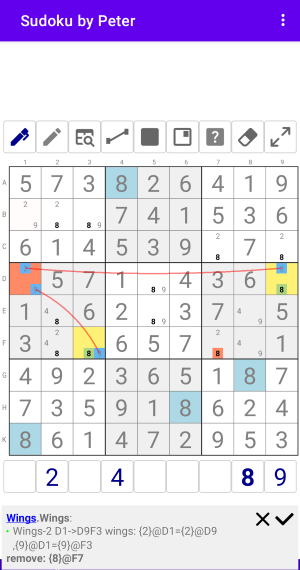Рис. 2.1. XY-Wings

Wings:Wings-2 D1->D9F3 wings: {2}@D1={2}@D9,{9}@D1={9}@F3 remove: {8}@F7

На рисунке...

Базовая ячейка: D1 с кандидатами {2,9}.

Правильные кралья:

1. {2}@D1={2}@D9 в Строке D.
2. {9}@D1={9}@F3 в Боксе 4.

Удаляемый кандидат: {8}@F7.

XYZ-Wings

В отличие от предыдущего метода XY-Wings в этом методе базовая ячейка содержит кандидата из неправильного крыла.

Признаки метода XYZ-Wings:

1. Используюся три свободных ячейки.
2. Одна базовая, из которой начинаются правильные крылья. В этом методе крылья могут быть только линками (сильными или слабыми)
3. Базовая ячейка содержит кандидатов из правильных крыльев и кандидата из неправильного крыла.
4. Две свободные ячейки с окончаниями крыльев.
5. Есть одно неправильное крыло.
6. Все узлы неправильного крыла имеют как минимум одного общего соседа. Эти узлы можно удалять.

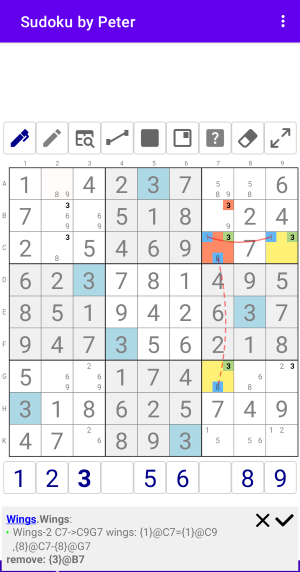Рис. 3.1. XYZ-Wings

Wings:Wings-2 C7->C9G7 wings: {1}@C7={1}@C9,{8}@C7-{8}@G7 remove: {3}@B7

На рисунке...

Базовая ячейка: C7 с кандидатами {1,3,8}.

Правильные кралья:

1. {1}@C7={1}@C9 в Строке C.
2. {8}@C7-{8}@G7 в Столбце 7.

Удаляемый кандидат: {3}@B7.

WXYZ-Wing

Признаки метода WXYZ-Wings:

1. Используюся четыре свободных ячейки.
2. Одна базовая, из которой начинаются правильные крылья. В этом методе крылья могут содержать более 2 узлов.
3. Базовая ячейка содержит кандидатов из правильных крыльев и может кандидата из неправильного крыла.
4. Три свободные ячейки с окончаниями крыльев.
5. Есть одно неправильное крыло.
6. Все узлы неправильного крыла имеют как минимум одного общего соседа. Эти узлы можно удалять.

WXYZ-Wing Пример 1

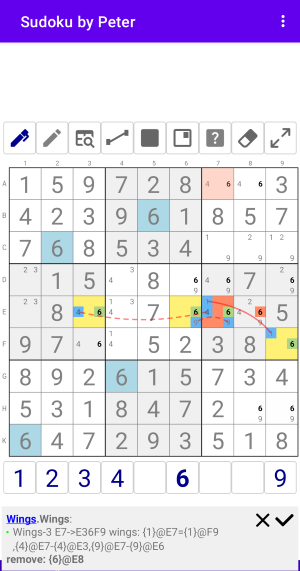Рис. 4.1. WXYZ-Wings 1

Wings:Wings-3 E7->E36F9 wings: {1}@E7={1}@F9,{4}@E7-{4}@E3,{9}@E7-{9}@E6 remove: {6}@E8

На рисунке...

Базовая ячейка: E7 с кандидатами {1,4,6,9}.

Правильные кралья:

1. {1}@E7={1}@F9 в Боксе 6.
2. {4}@E7-{4}@E3 в Строке E.
3. {9}@E7-{9}@E6 в Строке E.

Удаляемый кандидат: {6}@E8.

WXYZ-Wing Пример 2

Пример со сложным крылом, состоящим из трех узлов. В примере это крыло с цифрой 4 в Боксе 1.

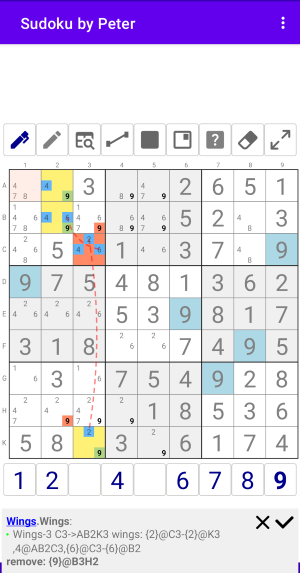Рис. 5.1. WXYZ-Wings 2

Wings:Wings-3 C3->AB2K3 wings: {2}@C3-{2}@K3,4@AB2C3,{6}@C3-{6}@B2 remove: {9}@B3H2

На рисунке...

Базовая ячейка: C3 с кандидатами {2,4,6}.

Правильные кралья:

1. {2}@C3-{2}@K3.
2. 4@AB2C3.
3. {6}@C3-{6}@B2.

Удаляемые кандидаты: {9}@B3H2.

W-Wings

Должно быть два параллельных крыла, связанных сильным линком. На других концах крыльев должна быть Петля (Hinge) c парой одинаковых кандидатов.

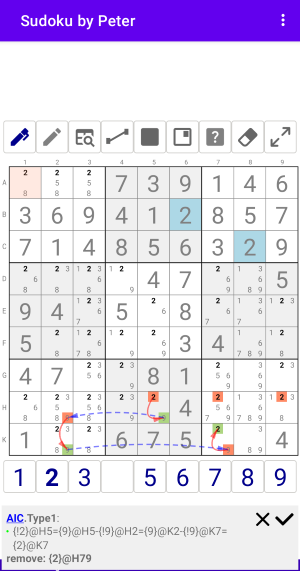Рис. 6.1. W-Wings

AIC:Type1 {!2}@H5={9}@H5-{!9}@H2={9}@K2-{!9}@K7={2}@K7 remove: {2}@H79

На текущий момент мне кажется, что это частный случай AIC Type1 размера 5.

---

Далее приводятся примеры с разным количеством крыльев из одной Базовой ячейки.

Обозначение Wings-xN, где N - количество крыльев.

При этом получается:

• N+1 - задействованных ячеек
• N - правильных крыльев.
• 1 - неправильное крыло
• N+1 - задействованных кандидатов

Wings-x2

Wings-x2 с одной базовой ячейкой и 2 крыльями

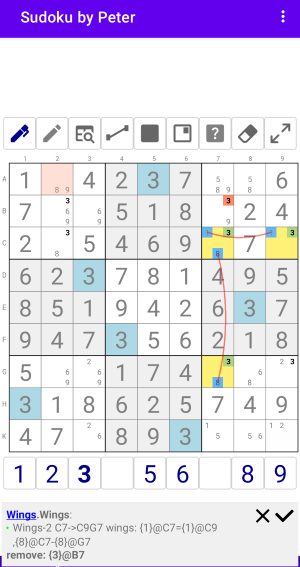Рис. 7.1. Wings x2

Wings:Wings-2 C7->C9G7 wings: {1}@C7={1}@C9,{8}@C7-{8}@G7 remove: {3}@B7

Wings-x3

Wings-x3 с одной базовой ячейкой и 3 крыльями

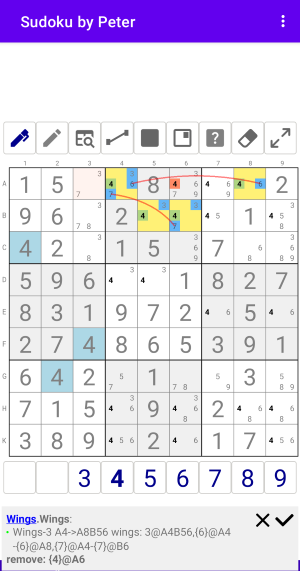Рис. 8.1. Wings x3

Wings:Wings-3 A4->A8B56 wings: 3@A4B56,{6}@A4-{6}@A8,{7}@A4-{7}@B6 remove: {4}@A6

Wings-x4

Wings-x4 с одной базовой ячейкой и 4 крыльями

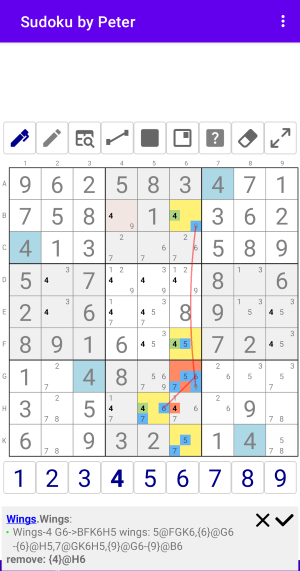Рис. 9.1. Wings x4

Wings:Wings-4 G6->BFK6H5 wings: 5@FGK6,{6}@G6-{6}@H5,7@GK6H5,{9}@G6-{9}@B6 remove: {4}@H6

Wings-x5

Внимание!

Возможно, других примеров с пятью крыльями в Интернете больше нет.

Wings-x5 с одной базовой ячейкой и 5 крыльями

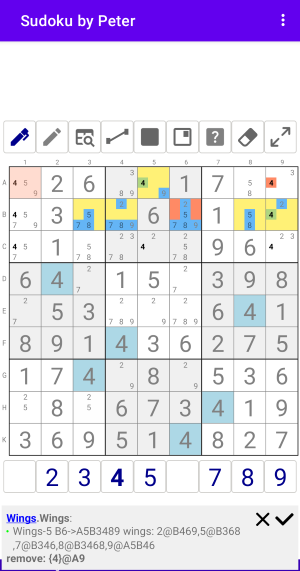Рис. 10.1. Wings x5

Wings:Wings-5 B6->A5B3489 wings: 2@B469,5@B368,7@B346,8@B3468,9@A5B46 remove: {4}@A9

Wings-x6

Внимание!

Возможно, других примеров с шестью крыльями в Интернете больше нет.

Пример Wings-x6 №1

Пример Wings-x6 №1 с одной базовой ячейкой и 6 крыльями

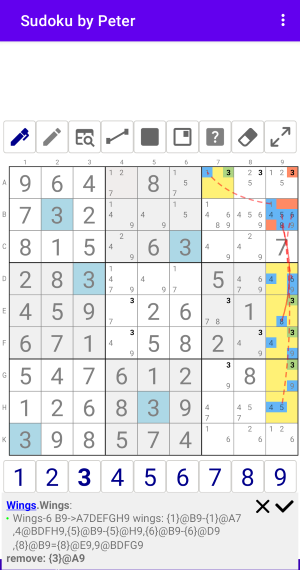Рис. 11.1. Wings x6 1

Wings:Wings-6 B9->A7DEFGH9 wings: {1}@B9-{1}@A7,4@BDFH9,{5}@B9-{5}@H9,{6}@B9-{6}@D9,{8}@B9={8}@E9,9@BDFG9 remove: {3}@A9

Пример Wings-x6 №2

Пример Wings-x6 №2 с одной базовой ячейкой и 6 крыльями

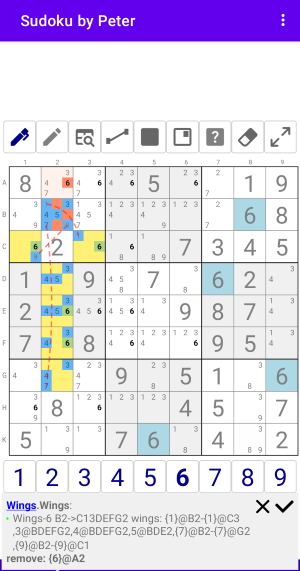Рис. 11.2. Wings x6 2

Wings:Wings-6 B2->C13DEFG2 wings: {1}@B2-{1}@C3,3@BDEFG2,4@BDEFG2,5@BDE2,{7}@B2-{7}@G2,{9}@B2-{9}@C1 remove: {6}@A2