Метод решения судоку Forcing Chains

В методе Forcing Chains из Одного или Нескольких предположений по нескольким цепочкам приводящих к Заключению, можно сделать определенный Вывод.

Предположение -(по цепочкам)-> Заключение => Вывод

---

Определение и описание одной Цепочки / Chain

---

Варианты Forcing Chains:

1. (Предположение - Единственное значение) => Ошибка. Это значит, что Предположение - неверно. Соответственно решением будет Обратное значение Предположения.
2. (Предположение - Полное множество, включающее правильный ответ) => Единственное значение (Решение). Это значит, что Единственное значение - верно.
3. (Предположение - Полное множество, включающее правильный ответ) => Несколько Решений, исключающие другие варианты. Это значит, что другие варианты являются неправильными.

Предположения

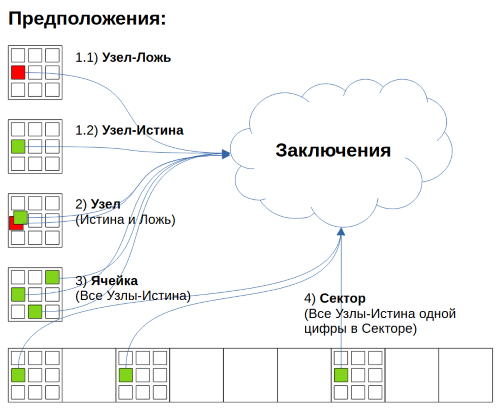Рис. 1. Forcing chains: Предположения

Предположения (Источники цепочек) - одно или несколько предположений, на основе которых можно сделать Заключение.

Предположения могут быть единственными или полное множество возможных вариантов.

Типы предположений:

1. Единственный источник - Узел-Истинности (Ложь или Истина)
2. Полное множество значений, охватывающее все возможные варианты, включающее в себя правильное решение.

Предположение - Единственное значение

1. Узел-Истинности (NodeTruth): Узел-Истина или Узел-Ложь (NodeTrue или NodeFalse)

Предположение - Полное множество

1. Узел (Node) - Узел-Ложь, Узел-Истина (NodeTrue, NodeFalse)
2. Ячейка (Cell) - Узлы-Истины (NodesTrue) всех кандидатов в Ячейке
3. Сектор (Sector) - Узлы-Истины (NodesTrue) всех кандидатов одной цифры в Секторе

Предположение 1. Узел-Истинности (NodeTruth)

Рис. 1. Forcing chains: Предположение Узел-Ложь или Узел-Истина

Источником цепочек может быть Узел-Истинности (Узел-кандидат в конкретном значении Истина или Ложь)

Предположение 2. Узел / Node (NodeTrue и NodeFalse)

Рис. 2. Forcing chains: Предположение Узел

Источником цепочек может быть Узел-кандидат во всех возможных значениях, т.е. Истина и Ложь

Предположение 3. Все узлы в Ячейке

Рис. 3. Forcing chains: Предположение Узлы-Истина в одной ячейке

Источником цепочек могут быть все возможные Узлы-Истина кандидатов в ячейке. Это множество обязательно будет включать правильный узел.

Предположение 4. Кандидат в Секторе

Рис. 4. Forcing chains: Предположение Узлы-Истина одной цифры в секторе

Источником цепочек могут быть все возможные Узлы-кандидаты одной цифры в значении Истина. Это множество обязательно будет включать правильный узел.

Заключения

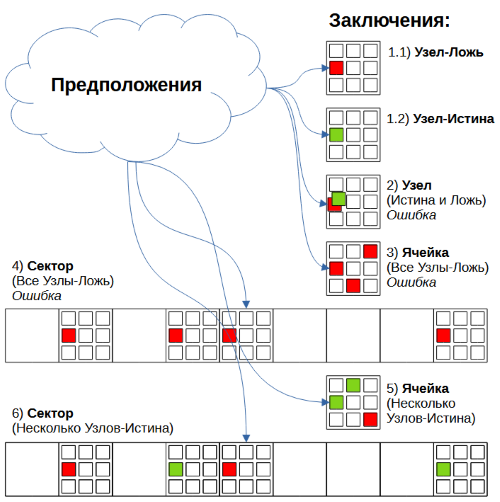Рис. 2. Forcing chains: Заключения

Возможные варианты окончания цепочек, на основе которых можно сделать вывод о предположении.

Заключение 1. Узел-Истинности.

Рис. 4. Forcing chains: Заключение Узел-Истинности (Ложь или Истина)

Если все возможные варианты, включающие правильны ответ приводят к одному Узлу-истинности.

Заключение 2. Несколько Узлов-Истин во множестве возможных

Рис. 5. Forcing chains: Заключение Несколько Узлов-Истина одной цифры в секторе

Несколько Узлов-Истин в Секторе для одной цифры или в Ячейке для разных цифр

Заключение 3. Все Узлы-Ложь во множестве возможных

Рис. 6. Forcing chains: Заключение Все Узлы-Ложь одной цифры в секторе

Ошибочное заключение. Если какое-нибудь предположение приводит к таком Ошибочному заключению, то предположение неверно.

Заключение 4. Deadly Pattern

Если Узел-Истинности приводит к Узлам-Истины, образующие Deadly Pattern, то такой Узел-Истинности неверный.

1.1. NodeTruth-TrueFalseInNode (Forcing chains)

Схема

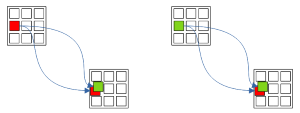Рис. 1.1. Forcing chains: Узел-Истинности -> Один Узел Истина и Ложь

Пример 1.1.1

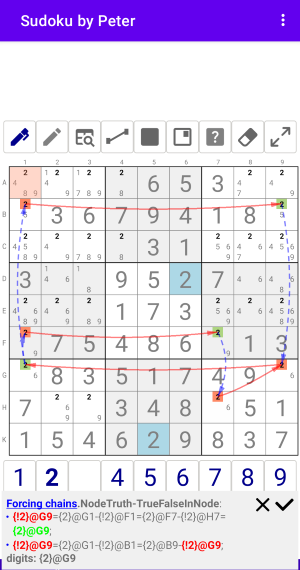Рис. 1.1.1. Forcing chains: NodeTruth-NodesTrueInSector

Цепочки из одного Узла-Истинности в один Узел с взаимоисключающими значениями (Истина и Ложь).

Решение:
Forcing chains:NodeTruth-TrueFalseInNode

1. {!2}@G9={2}@G1-{!2}@F1={2}@F7-{!2}@H7={2}@G9;
2. {!2}@G9={2}@G1-{!2}@B1={2}@B9-{!2}@G9;

digits: {2}@G9

Пример 1.1.2

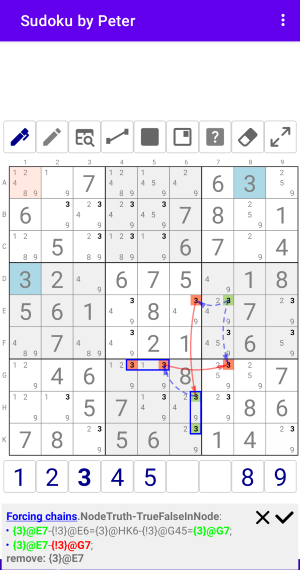Рис. 1.1.2. Forcing chains: NodeTruth-NodesTrueInSector

Цепочки из одного Узла-Истинности в один Узел с взаимоисключающими значениями (Истина и Ложь).

Решение:
Forcing chains:NodeTruth-TrueFalseInNode

1. {3}@E7-{!3}@E6={3}@HK6-{!3}@G45={3}@G7;
2. {3}@E7-{!3}@G7;

remove: {3}@E7

1.2. NodeTruth-NodesTrueInCell (Forcing chains)

Схема

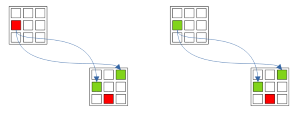Рис. 1.2. Forcing chains: Узел-Истинности -> Один Узел Истина и Ложь

Если цепочки из одного Node-True приводят к нескольким взаимоисключающим Узлам-True, то такое предположение неверно.

Пример 1.2.1

Цепочки из Узла-Ложь в Несколько Узлов-Истина в Ячейке.

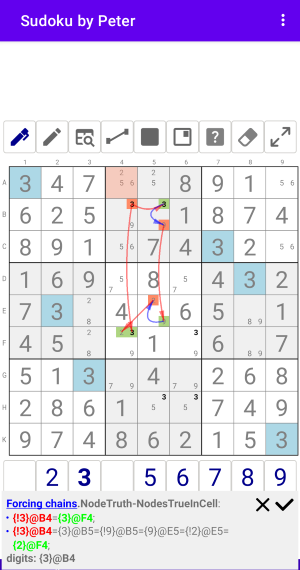Рис. 1.2.1. Forcing chains: NodeFalse-NodesTrueInCell

Решение:
Forcing chains:NodeTruth-NodesTrueInCell

1. {!3}@B4={3}@F4;
2. {!3}@B4={3}@B5={!9}@B5={9}@E5={!2}@E5={2}@F4;

digits: {3}@B4

Пример 1.2.2

Цепочки из Узла-Истины в Несколько Узлов-Истина в Ячейке.

1. {2}@C3-{!1}@C3={1}@C6;
2. {2}@C3-{!2}@B3={2}@B6={!9}@B6={9}@C6;

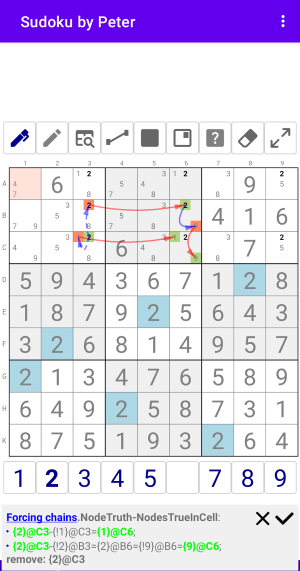Рис. 1.2.2. Forcing chains: NodeTrue-NodesTrueInCell

Решение:
Forcing chains:NodeTruth-NodesTrueInCell

1. {2}@C3-{!1}@C3={1}@C6;
2. {2}@C3-{!2}@B3={2}@B6={!9}@B6={9}@C6;

remove: {2}@C3

1.3. NodeTruth-NodesFalseInCell (Forcing chains)

Схема

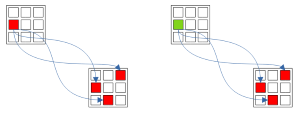Рис. 1.3. Forcing chains: Узел-Истиности -> Все Узлы-Ложь в ячейке

Если цепочки из одного Node-True приводят ко всем всевозможным Узлам-False, то такое предположение неверно.

Пример 1.3.1

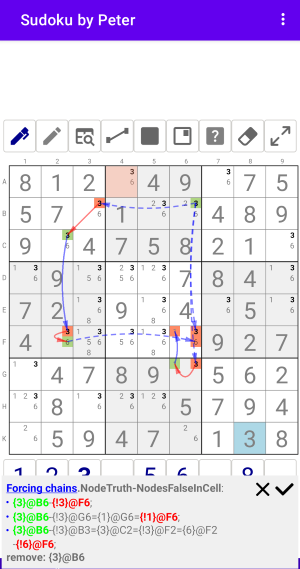Рис. 1.3.1. Forcing chains: NodeFalse-NodesFalseInCell

Цепочки из Узла-Ложь ко всем возможным Узлам-Ложь в Ячейке. Т.е. в ячейке ничего не остается, это ошибочная ситуация, поэтому предположение неверное.

Решение:
Forcing chains:NodeTruth-NodesFalseInCell

1. {!6}@D1={6}@D9-{!6}@F9;
2. {!6}@D1={6}@E1={!9}@E1={9}@E9={!9}@F9;

digits: {6}@D1

Пример 1.3.2

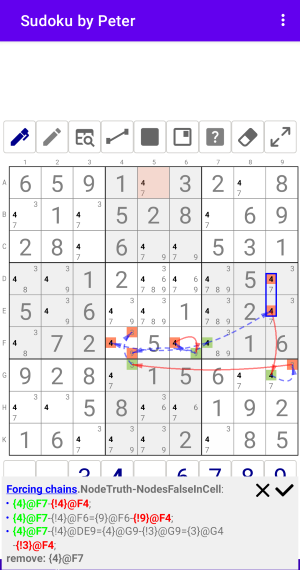Рис. 1.3.2. Forcing chains: NodeTrue-NodesFalseInCell

Цепочки из Узла-Истина ко всем возможным Узлам-Ложь в Ячейке. Т.е. в ячейке ничего не остается, это ошибочная ситуация, поэтому предположение неверное.

Решение:
Forcing chains:NodeTruth-NodesFalseInCell

1. {3}@B6-{!3}@F6;
2. {3}@B6-{!3}@G6={1}@G6={!1}@F6;
3. {3}@B6-{!3}@B3={3}@C2={!3}@F2={6}@F2-{!6}@F6

remove: {3}@B6

1.4. NodeTruth-NodesTrueInSector (Forcing chains)

Схема

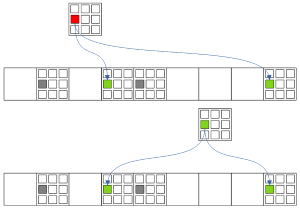Рис. 1.4. Forcing chains: Узел-Истина -> Несколько взаимоисключающихся Узлов-Истина в секторе

Цепочки из одного Узла-Истинности в Несколько Узлов-Истина в Секторе.

Пример 1.4.1

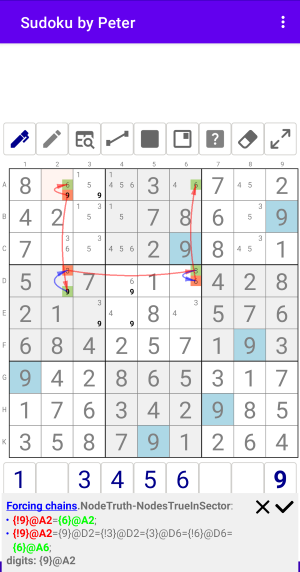Рис. 1.4.1. Forcing chains: NodeFalse-NodesTrueInSector

Решение:
Forcing chains:NodeTruth-NodesTrueInSector

1. {!9}@A2={6}@A2;
2. {!9}@A2={9}@D2={!3}@D2={3}@D6={!6}@D6={6}@A6;

digits: {9}@A2

Пример 1.4.2

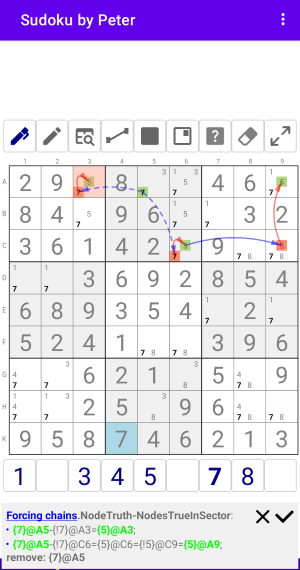Рис. 1.4.2. Forcing chains: NodeTrue-NodesTrueInSector

Решение:
Forcing chains:NodeTruth-NodesTrueInSector

1. {7}@A5-{!7}@A3={5}@A3;
2. {7}@A5-{!7}@C6={5}@C6={!5}@C9={5}@A9;

remove: {7}@A5

1.5. NodeTruth-NodesFalseInSector (Forcing chains)

Схема

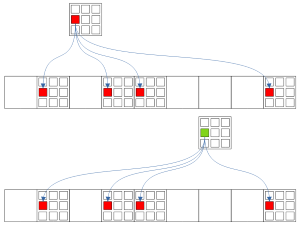Рис. 1.5. Forcing chains: Узел-Истина -> Все Узлы-Ложь одной цифры в секторе

Пример 1.5.1

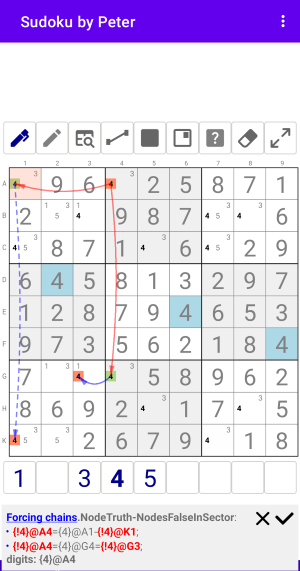Рис. 1.5.1. Forcing chains: NodeFalse-NodesFalseInSector

Решение:
Forcing chains:NodeTruth-NodesFalseInSector

1. {!4}@A4={4}@A1-{!4}@K1;
2. {!4}@A4={4}@G4={!4}@G3;

к 4 в Box7

digits: {4}@A4

Пример 1.5.2

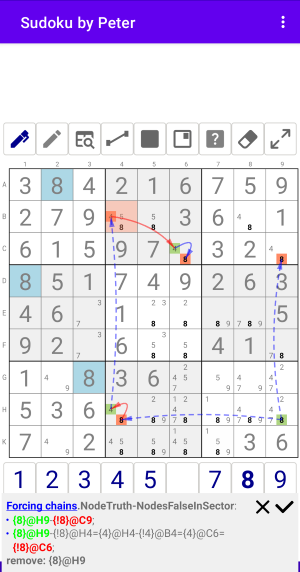Рис. 1.5.2. Forcing chains: NodeFalse-NodesFalseInSector

Решение:
Forcing chains:NodeTruth-NodesFalseInSector

1. {8}@H9-{!8}@C9;
2. {8}@H9-{!8}@H4={4}@H4-{!4}@B4={4}@C6={!8}@C6;

к 8 в RowC

remove: {8}@H9

2.1. TrueFalseInNode-NodeTruth (Forcing chains)

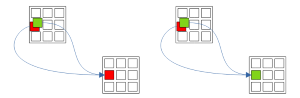Рис. 2.1. Forcing chains: Из Узла(Ложь и Истина) -> Узел-Истинности

Если цепочки из всех значений (Истина/Ложь) Узла (Node) приводят к одному Узлу-Истинности, то этот Узел-истинности - правильное решение.

Пример 2.1.1

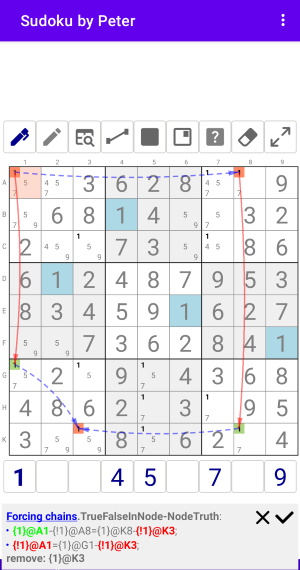Рис. 2.1.1. Forcing chains: TrueFalseInNode-NodeFalse

Решение:
Forcing chains:TrueFalseInNode-NodeTruth

1. {1}@A1-{!1}@A8={1}@K8-{!1}@K3;
2. {!1}@A1={1}@G1-{!1}@K3;

remove: {1}@K3

Пример 2.1.2

Рис. 2.1.2. Forcing chains: TrueFalseInNode-NodeTrue

Решение:
Forcing chains:TrueFalseInNode-NodeTruth

1. {4}@A1-{!4}@B3={4}@B9;
2. {!4}@A1={5}@A1={!5}@A7={5}@C9={!4}@C9={4}@B9;

digits: {4}@B9

2.2. TrueFalseInNode-NodesTrueInCell (Forcing chains)

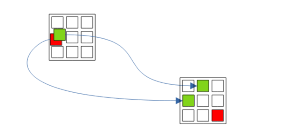Рис. 2.2. Forcing chains: Из Узла(Ложь и Истина) -> Несколько Узлов-Истина в Ячейке

Пример 2.2.1

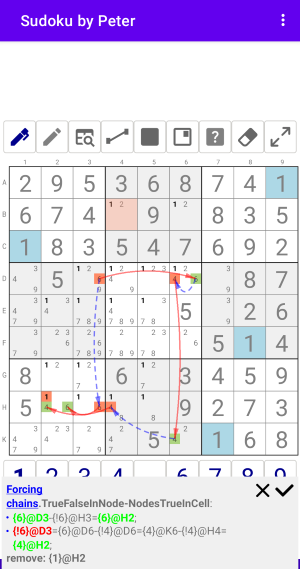Рис. 2.2.1. Forcing chains: TrueFalseInNode-NodesTrueInCell

Решение:
Forcing chains:TrueFalseInNode-NodesTrueInCell

1. {6}@D3-{!6}@H3={6}@H2;
2. {!6}@D3={6}@D6-{!4}@D6={4}@K6-{!4}@H4={4}@H2;

remove: {1}@H2

2.3. TrueFalseInNode-NodesTrueInSector (Forcing chains)

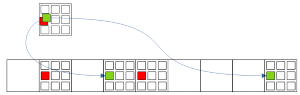Рис. 2.3. Forcing chains: Из Узла(Ложь и Истина) -> Несколько Узлов-Истина для одной цифры в Секторе

Пример 2.3.1

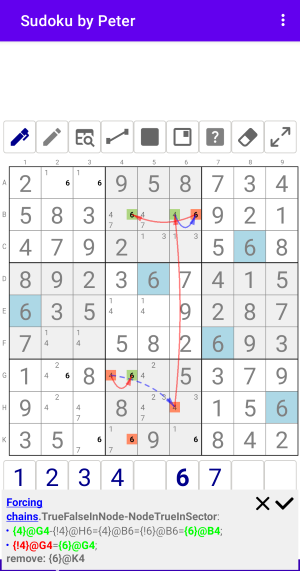Рис. 2.3.1. Forcing chains: TrueFalseInNode-NodeTrueInSector

Решение:
Forcing chains:TrueFalseInNode-NodeTrueInSector

1. {4}@G4-{!4}@H6={4}@B6={!6}@B6={6}@B4;
2. {!4}@G4={6}@G4;

to: Col4

remove: {6}@K4

3.1. Cell-NodeTruth (Forcing chains)

Схема

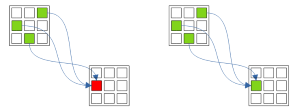Рис. 3.1. Forcing chains: Все Узлы-Истина в ячейке -> Узел-Истинности

Если от каждого Узла-Истины в Ячейке есть цепочка, указывающая на один Узел-Истинности, то это Состояние для Узла можно принимать за правильное.

Пример 3.1.1

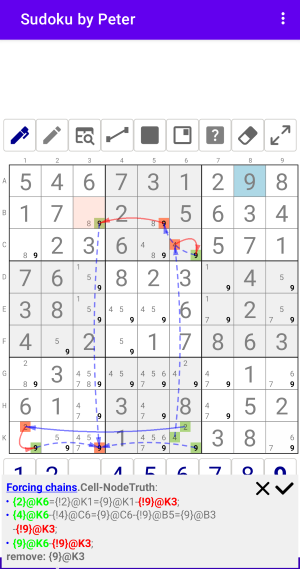Рис. 3.1.1. Forcing chains: Cell-NodeFalse

Решение:
Forcing chains:Cell-NodeTruth

1. {2}@K6={!2}@K1={9}@K1-{!9}@K3;
2. {4}@K6-{!4}@C6={9}@C6-{!9}@B5={9}@B3-{!9}@K3;
3. {9}@K6-{!9}@K3

remove: {9}@K3

Рассмотрим приведенный выше пример. В ячейке K6 есть три узла {246}@K6. Для каждого из этих Узлов-Истины есть цепочка, которая приводит к одному Узлу-Ложь. Так как цепочки рассматривают все возможные варианты в ячейке K6, значит {9}@K3 будет Ложь. Убираем этого кандидата.

Пример 3.1.2

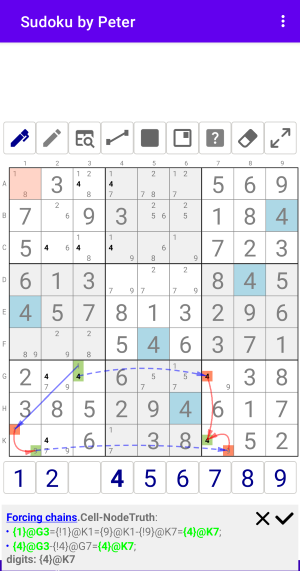Рис. 3.1.2. Forcing chains: Cell-NodeFalse

Решение:
Forcing chains:Cell-NodeTruth

1. {1}@G3={!1}@K1={9}@K1-{!9}@K7={4}@K7;
2. {4}@G3-{!4}@G7={4}@K7;

digits: {4}@K7

3.2. Cell-Cell (Forcing chains)

Схема

Рис. 1. Forcing chains: Все Узлы-Истина в ячейке -> Несколько Узлов-Истина в ячейке

Если от каждого Узла-Истины в Ячейке есть цепочки, указывающие на несколько Узелов-Истина в другой ячейке, то остальных кандидатов можно убирать.

Пример 3.2.1

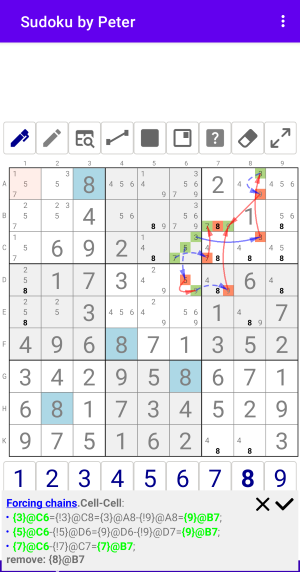Рис. 3.2.1. Forcing chains: Cell-Cell

На рисунке...

Решение:
Forcing chains:Cell-Cell

1. {7}@C6-{!7}@C7={7}@B7;
2. {3}@C6={!3}@C8={3}@A8-{!9}@A8={9}@B7;

remove: {8}@B7

3.3. Cell-Sector (Forcing chains)

Схема

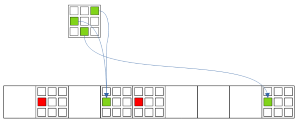Рис. 3.3.1. Forcing chains: Все Узлы-Истина в ячейке -> Несколько Узлов-Истина одной цифры в секторе

Если от каждого Узла-Истины в Ячейке есть цепочки, указывающие на несколько Узелов-Истина в другой ячейке, то остальных кандидатов можно убирать.

Пример 3.3.1

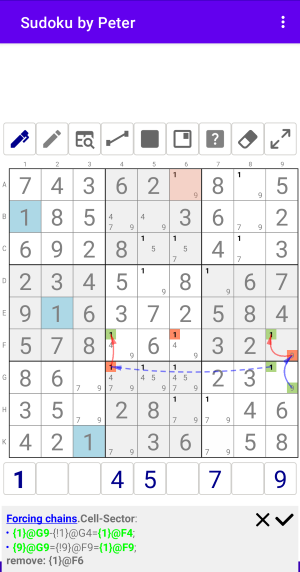Рис. 3.2.1. Forcing chains: Cell-Sector

На рисунке...

Решение:
Forcing chains:Cell-Sector

1. {1}@G9-{!1}@G4={1}@F4;
2. {9}@G9={!9}@F9={1}@F9;

to: RowF remove: {1}@F6

4.1. Sector-NodeTruth (Forcing chains)

Схема

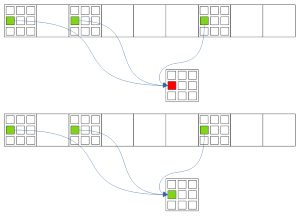Рис. 4.1. Forcing chains: Все Узлы-Истина одной цифры в секторе -> Узел-Истинности

Если от каждого Узла-Истины одного кандидата в Секторе есть цепочка, указывающая на один Узел-Истинности, то это Состояние для Узла можно принимать за правильное.

Пример 4.1.1

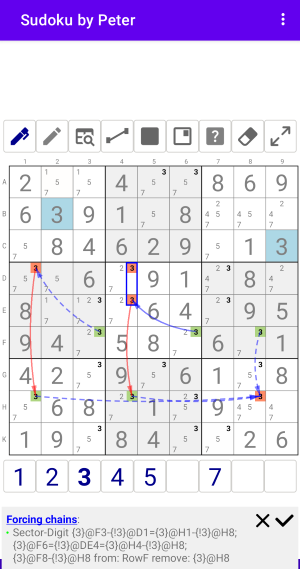Рис. 4.1.1. Forcing chains: Sector-NodeFalse

Решение:
Forcing chains: Sector-Digit from: RowF

• {3}@F3-{!3}@D1={3}@H1-{!3}@H8;
• {3}@F6={!3}@DE4={3}@H4-{!3}@H8;
• {3}@F8-{!3}@H8

remove: {3}@H8

Рассмотрим приведенный выше пример. В Строке F есть 3 Узла для кандидата 3. Для каждого Узла-Истины есть цепочка, которая приводит к одному Узлу-Ложь. Так как цепочки рассматривают все возможные варианты 3 в Строке F, значит {3}@H8 будет Ложь. Убираем этого кандидата.

Пример 4.1.2

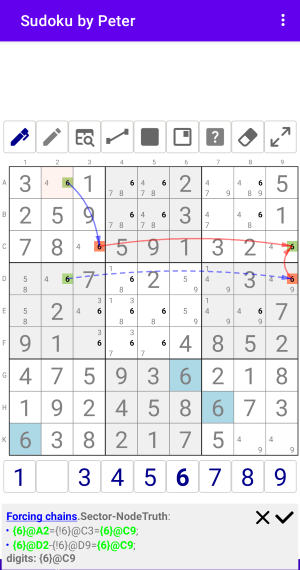Рис. 4.1.2. Forcing chains: Sector-NodeTrue

Решение:
Forcing chains: Sector-Digit from: Col2

1. {6}@A2={!6}@C3={6}@C9;
2. {6}@D2-{!6}@D9={6}@C9;

digits: {6}@C9

4.2. Sector-Cell (Forcing chains)

Схема

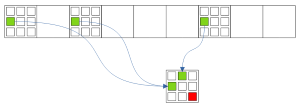Рис. 4.2. Forcing chains: Все Узлы-Истина одной цифры в секторе -> Несколько Узлов-Истина в ячейке

Если от каждого Узла-Истины одного кандидата в Секторе есть цепочка, указывающая на несколько Узлов-Истина в Ячейке, то остальные Узлы в этой Ячейке можно убирать.

Пример 4.2.1

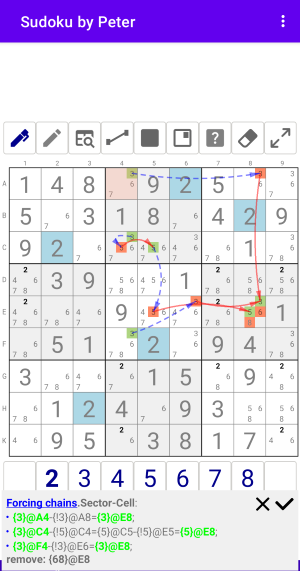Рис. 15. Forcing chains: Sector-Cell

От всех Узлов 3 в Столбце 4 идут цепочки к нескольким Узлам-Истины в ячейке E8:

Решение:
Forcing chains:Sector-Cell from: Col4

1. {3}@A4-{!3}@A8={3}@E8;
2. {3}@C4-{!5}@C4={5}@C5-{!5}@E5={5}@E8;
3. {3}@F4-{!3}@E6={3}@E8

remove: {6}@E8,{8}@E8

4.3. Sector-Sector (Forcing chains)

Схема

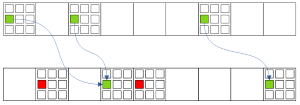Рис. 4.3. Forcing chains: Все Узлы-Истина одной цифры в секторе -> Несколько Узлов-Истина одной цифры в секторе

Если от каждого Узла-Истины одного кандидата в Секторе есть цепочка, указывающая на несколько Узлов-Истина одной цифры в Секторе, то остальные Узлы во втором Секторе можно убирать.

Пример 4.3.1

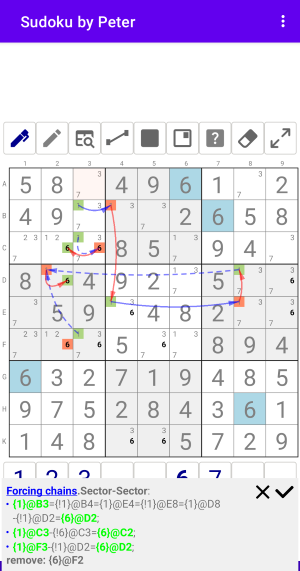Рис. 4.3.1. Forcing chains: Sector-Sector

На рисунке...

Из всех узлов цифры 1 в Столбце 3 идут цепочки только к двум узлам цифры 6 в Столбце 2 => Остальные узлы цифры 6 в Столбце 2 можно удалять.

Решение:
Forcing chains:Sector-Sector from: Col3 to: Col2

1. {1}@B3={!1}@B4={1}@E4={!1}@E8={1}@D8-{!1}@D2={6}@D2;
2. {1}@C3-{!6}@C3={6}@C2;
3. {1}@F3-{!1}@D2={6}@D2

remove: {6}@F2